DeepSeek Math V2 Guide: Smarter AI for Real Math

Should you’ve been following the AI area currently, you’ve most likely seen one thing large: individuals don’t simply care what an AI solutions anymore, they care how it reaches that reply. And that’s precisely the place DeepSeek Math V2 steps in. It’s an open-source mannequin constructed particularly for actual mathematical reasoning.

On this information, I’ll stroll you thru what DeepSeek Math V2 is, why everyone seems to be speaking about its generator-verifier system, and the way this mannequin manages to unravel complicated proofs whereas checking its personal work like a strict math instructor. Should you’re inquisitive about how AI is lastly getting good at formal math, maintain studying.

What’s DeepSeek Math V2? 

DeepSeek Math V2 is DeepSeek-AI’s latest open-source LLM constructed particularly for mathematical reasoning and theorem proving. Launched on the finish of 2025, it marks an enormous shift from AI fashions that merely return remaining solutions to ones that really present their work and justify each step.

What makes it particular is its two-model generator–verifier setup. One mannequin writes the proof, and the second mannequin checks every step like a logic inspector. So as an alternative of simply fixing an issue, DeepSeek Math V2 additionally evaluates whether or not its personal reasoning is smart. The staff skilled it with reinforcement studying, rewarding not simply right solutions however clear, rigorous derivations.

And the outcomes converse for themselves. DeepSeek Math V2 performs on the high degree in main math competitions, scoring round 83.3% at IMO 2025 and 98.3% on the Putnam 2024. It surpasses earlier open fashions and comes surprisingly near the perfect proprietary programs on the market.

Key Options of DeepSeek Math V2 

• Huge scale: With 685B parameters constructed on DeepSeek-V3.2-ExpBase, the mannequin handles extraordinarily lengthy proofs utilizing a number of numeric codecs (BF16, F8_E4M3, F32) and sparse consideration for environment friendly computation.
• Self-verification: A devoted verifier checks each proof step for logical consistency. If a step is fallacious or a theorem is misapplied, the system flags it and the generator is retrained to keep away from repeating the error. This suggestions loop forces the mannequin to refine its reasoning.
• Reinforcement coaching: The mannequin was skilled on mathematical literature and artificial issues, then improved by means of proof-based reinforcement studying. The generator proposes options, the verifier scores them, and tougher proofs yield stronger rewards, pushing the mannequin towards deeper and extra correct derivations.
• Open supply and accessible: The weights are launched below Apache 2.0 and obtainable on Hugging Face and GitHub. You can too strive DeepSeek Math V2 straight by means of the free DeepSeek Chat interface, which helps non-commercial analysis and academic use.

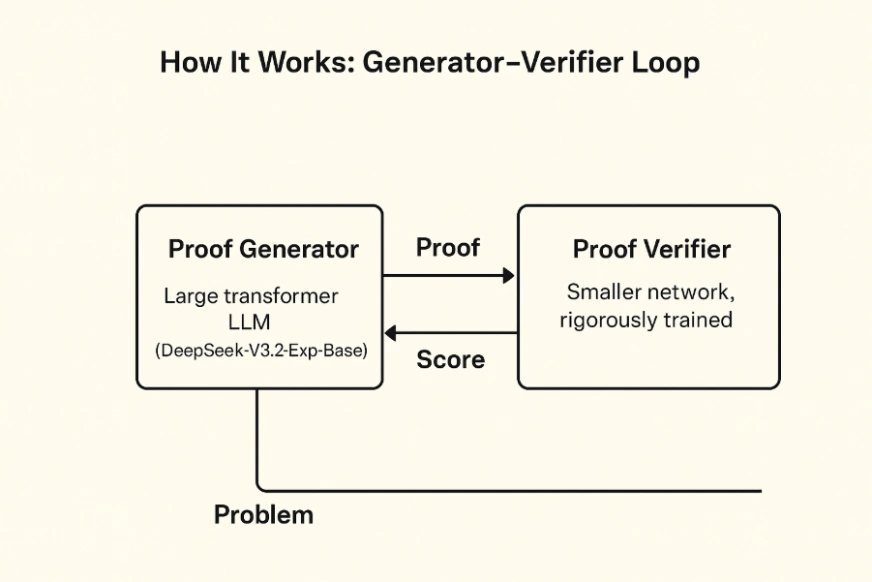
The Two-Mannequin Structure of DeepSeek Math V2

DeepSeek Math V2’s structure presents two principal elements that work together with one another: 

• Proof Generator: This huge transformer LLM (DeepSeek-V3.2-Exp-Base) is chargeable for creating step-by-step mathematical proofs based mostly on the issue assertion. 

• Proof Verifier: Though it’s a smaller community, it’s an extensively skilled one which represents each proof with logical steps (for instance, by way of an summary syntax tree) and carries out the appliance of mathematical guidelines on them. It signifies the inconsistencies within the reasoning or the invalid manipulations that aren’t termed as ‘phrases’ and assigns a “rating” to every proof. 

Coaching occurs in two phases. First, the verifier is skilled on recognized right and incorrect proofs. Then the generator is skilled with the verifier performing as its reward mannequin. Each time the generator produces a proof, the verifier scores it. Improper steps get penalized, absolutely right proofs get rewarded, and over time the generator learns to provide clear, legitimate derivations.

Multi-Go Verification and Search

Because the generator improves and begins producing tougher proofs, the verifier receives additional compute resembling extra search passes to catch subtler errors. This creates a transferring goal the place the verifier all the time stays barely forward, pushing the generator to enhance constantly.

Throughout regular operation, the mannequin additionally makes use of a multi-pass inference course of. It generates many candidate proof drafts, and the verifier checks every one. DeepSeek Math V2 can department in an MCTS-style search the place it explores totally different proof paths, removes those with low verifier scores, and iterates on the promising ones. In easy phrases, it retains rewriting its work till the verifier approves it.

def generate_verified_proof(downside):
    root = initialize_state(downside)
    whereas not root.is_complete():
        youngsters = develop(root, generator)
        for little one in youngsters:
            rating = verifier.consider(little one.proof_step)
            if rating < THRESHOLD:
                prune(little one)
        root = select_best(youngsters)
    return root.full_proof

DeepSeek Math V2 ensures that each reply comes with clear, step-by-step reasoning, due to its mixture of technology and real-time verification. It is a main improve from fashions that solely goal for the ultimate reply with out displaying how they reached it.

The right way to Entry DeepSeek Math 2?

The mannequin weights and code are publicly obtainable below an Apache 2.0 license (DeepSeek moreover mentions a non-commercial research-friendly license). To strive it out, you possibly can:  

• Obtain from Hugging Face: The mannequin is hosted on Hugging Face deepseek-ai/DeepSeekMath-V2 . Utilizing the Hugging Face Transformers library, one can load the mannequin and tokenizer. Consider it’s enormous, you’ll want no less than a number of high-end GPUs (the repo recommends 8×A100) or TPU pods for inference. 

• DeepSeek Chat interface: Should you don’t have large compute, DeepSeek provides a free internet demo at chat.deepseek.com . This “Chat with DeepSeek AI” permits interactive prompting (together with math queries) with out setup. It’s a simple strategy to see the mannequin’s output on pattern issues.  

• APIs and integration: You’ll be able to deploy the mannequin by way of any normal serving framework (e.g. DeepSeek’s GitHub has code for multi-pass inference). Instruments like Apidog or FastAPI may help wrap the mannequin in an API. For instance, one may create an endpoint /solve-proof that takes an issue textual content and returns the mannequin’s proof and verifier feedback. 

Now, let’s strive the mannequin out!

Job 1: Generate a Step-by-Step Proof

Conditions: 

1. GPU with no less than 40GB VRAM (e.g., A100, H100, or comparable). 
2. Python atmosphere (Python 3.10+) 
3. Set up newest variations of: 

pip set up transformers speed up bitsandbytes torch –improve 

Step 1: Select a Math Drawback 

For this hands-on, we’ll be utilizing the next downside which is quite common in math olympiads: 

Let a, b, c be constructive actual numbers such {that a} + b + c = 1. Show that a² + b² + c² ≥ 1/3.

Step 2: Python script to run the Mannequin 

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch

# Load mannequin and tokenizer
model_id = "deepseek-ai/DeepSeek-Math-V2"
tokenizer = AutoTokenizer.from_pretrained(model_id, trust_remote_code=True)
mannequin = AutoModelForCausalLM.from_pretrained(
    model_id,
    torch_dtype=torch.bfloat16,
    device_map="auto",
    trust_remote_code=True
)

# Immediate
immediate = """You might be DeepSeek-Math-V2, a competition-level mathematical reasoning mannequin.
Resolve the next downside step-by-step. Present an entire and rigorous proof.
Drawback: Let a, b, c be constructive actual numbers such {that a} + b + c = 1. Show that a² + b² + c² ≥ 1/3.
Answer:"""

# Tokenize and generate
inputs = tokenizer(immediate, return_tensors="pt").to(mannequin.machine)
outputs = mannequin.generate(
    **inputs,
    max_new_tokens=512,
    temperature=0.2,
    top_p=0.95,
    do_sample=True
)

# Decode and print end result
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("n=== Proof Output ===n")
print(output_text)

# Step 3: Run the script
# In your terminal, run the next command:
# python deepseek_math_demo.py

Or when you require then you possibly can take a look at it on the internet interface as properly. 

Output:  

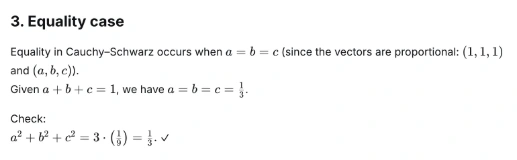
Job 2: Test the Correctness of a Mathematical Proof 

On this job, we’ll feed DeepSeek Math V2 a flawed math proof and ask its Verifier part to critique and validate the reasoning. It’s going to mainly present some of the vital options of DeepSeek Math V2, self-verification. 

Step 1: Outline the Drawback:

Step 2: Add the Verifier Immediate code:

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch

model_id = "deepseek-ai/DeepSeek-Math-V2"
tokenizer = AutoTokenizer.from_pretrained(model_id, trust_remote_code=True)
mannequin = AutoModelForCausalLM.from_pretrained(
    model_id,
    torch_dtype=torch.bfloat16,
    device_map="auto",
    trust_remote_code=True
)

# Incorrect proof for DeepSeek to confirm
incorrect_proof = """
Declare: For all actual numbers x, x^2 + 2x + 5 ≥ 0.
Proof: Since x^2 is all the time constructive and 2x + 5 is all the time constructive, their sum is all the time constructive. Therefore x^2 + 2x + 5 ≥ 0 for all actual x.
"""

immediate = f"""You're the DeepSeek Math V2 Verifier.
Your job is to critically analyze the next proof, establish incorrect reasoning,
and supply a corrected, rigorous clarification.
Proof to confirm:
{incorrect_proof}
Please present:
1. Whether or not the proof is right or incorrect.
2. Which steps include errors.
3. A corrected proof.
"""

inputs = tokenizer(immediate, return_tensors="pt").to(mannequin.machine)
outputs = mannequin.generate(
    **inputs,
    max_new_tokens=600,
    temperature=0.2,
    top_p=0.95,
    do_sample=True
)

print("n=== Verifier Output ===n")
print(tokenizer.decode(outputs[0], skip_special_tokens=True))

# Step 3: Run the script
# In your terminal, run the next command:
# python deepseek_verifier_demo.py 

Output: 

Efficiency and Benchmarks 

DeepSeek Math V2 delivers standout outcomes throughout main math benchmarks:

• Worldwide Math Olympiad (IMO) 2025: Scored round 83.3 % by absolutely fixing issues 1 to five and partially fixing downside 6. This matches high closed-source programs, even earlier than its official contest entry.
• Canadian Math Olympiad (CMO) 2024: Scored about 73.8 % by absolutely fixing 4 of 6 issues and partially fixing the remainder.
• Putnam Examination 2024: Achieved 98.3 % (118 out of 120 factors) below scaled compute, solely lacking partial credit score on the hardest questions.
• ProofBench (DeepMind): Acquired about 99 % approval on fundamental proofs and 62 % on superior proofs, outperforming GPT-4, Claude 4, and Gemini on structured reasoning.

In side-by-side comparisons, DeepSeek Math V2 constantly beats main fashions on proof accuracy by 15 to twenty %. Many fashions nonetheless guess or skip steps, whereas DeepSeek’s strict verification loop reduces error charges considerably, with studies displaying as much as 40 % fewer reasoning errors than speed-focused programs.

Functions and Significance 

DeepSeek Math V2 is not only sturdy in competitions. It pushes AI nearer to formal verification by treating each downside as a proof-checking job. Listed below are the principle methods it may be used:

• Schooling and tutoring: It could possibly grade math assignments, test pupil proofs, and supply step-by-step hints or apply issues.
• Analysis help: Helpful for exploring early concepts, recognizing weak reasoning, and producing new approaches in areas like cryptography and quantity idea.
• Theorem-proving programs: It could possibly help instruments like Lean or Coq by serving to translate natural-language reasoning into formal proofs.
• High quality management: It could possibly confirm complicated calculations in fields resembling aerospace, cryptography, and algorithm design the place accuracy is crucial.

Also Learn:

Conclusion 

DeepSeek Math V2 is a strong device amongst AI’s math-related duties. It connects an unlimited transformer spine with new proof-checking loops, achieves document scores in contests, and is made obtainable to the neighborhood totally free. The event of AI has all the time been the case in DeepSeek Math V2 that self-verifying is the core of deep considering, not solely of bigger fashions or knowledge.

Attempt it out as we speak and let me know your ideas within the remark part beneath!